Question

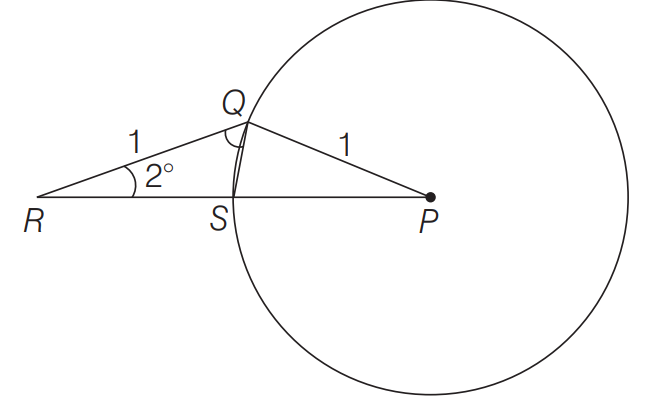
Suppose $Q$ is a point on the circle with centre $P$ and radius $1$ , as shown in the figure, $R$ is a point outside the circle such that $Q R=1$ and $\angle Q R P=2^{\circ}$. Let $S$ be the point where the segment $R P$ intersects the given circle. Then, measure of $\angle R Q S$ equals

• A. $86^{\circ}$
• B. $87^{\circ}$
• C. $88^{\circ}$
• D. $89^{\circ}$

Answer 1

Answer: (B)

$ \angle Q R P =2^{\circ} $
$ P Q =Q R=1 $
$\therefore \angle Q P R =2^{\circ} $
$ \angle R Q P =180^{\circ}-4^{\circ}=176^{\circ} $
$ S P =S Q $ radii of circle
$\therefore \angle S Q P =\angle Q S P $
$=\frac{180^{\circ}-2^{\circ}}{2} $
$=\frac{178^{\circ}}{2}=89^{\circ} $
$ \angle R Q S =\angle R Q P-\angle S Q P $
$=176^{\circ}-89^{\circ}=87^{\circ}$