Q.
Suppose $f(x)$ is a real valued polynomial function of degree 6 satisfying the following condition
(a) ' $f$ ' has minimum value at $x=0$ & 2
(b) ' $f$ ' has maximum value at $x =1$
(c) for all $x, \underset{x \rightarrow 0} {\text{Lim}}\frac{1}{x} \ln \begin{vmatrix}f(x) / x & 1 & 0 \\ 0 & 1 / x & 1 \\ 1 & 0 & 1 / x\end{vmatrix}=2$
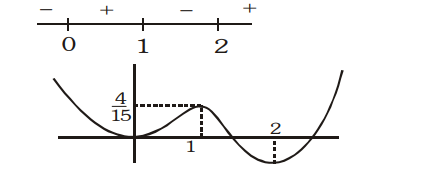
Number of solutions of the equation $8 f(x)-1=0$ is -
Application of Derivatives
Solution:
$\underset{x \rightarrow 0}{\text{Lt}} \frac{1}{x} \ln \begin{vmatrix}\frac{f(x)}{x} & 1 & 0 \\ 0 & \frac{1}{x} & 1 \\ 1 & 0 & \frac{1}{x}\end{vmatrix}=2$
$\underset{x \rightarrow 0}{\text{Lt}}\frac{1}{x} \ln \left(\frac{f(x)}{x^3}+1\right)=2 ....$(1)
for limit to exist
$\underset{x \rightarrow 0}{\text{Lt}} \frac{f(x)}{x^3}=0$
$\Rightarrow f(x)=a_0 x^6+a_1 x^5+a_2 x^4 $
Also $ f^{\prime}(0)=f^{\prime}(2)=f^{\prime}(1)=0$
$ f^{\prime}(x)=6 a_0 x^5+5 a_1 x^4+4 a_2 x^3 $
$=x^3\left(6 a_0 x^2+5 a_1 x+4 a_2\right) $
$ f^{\prime}(2)=0 $
$ \Rightarrow 24 a_0+10 a_1+4 a_2=0 $......(2)
$ f^{\prime}(1)=0 $
$ 6 a_0+5 a_1+4 a_2=0$.......(3)
Consider $e^{ n } \cdot(1)$
$\ln \left\{\underset{x \rightarrow 0}{\text{Lt}} \left(\frac{f(x)}{x^3}+1\right)^{\frac{1}{x}}\right\}=2$
$\ln e^{\left(\displaystyle\lim _{x \rightarrow 0} \frac{ f ( x )}{ x ^4}\right)}=2 \Rightarrow \underset{x \rightarrow 0}{\text{Lt}} \frac{ a _0 x ^6+ a _1 x ^5+ a _2 x ^4}{ x ^4}=2$
$\Rightarrow a _2=2$
Putting $a_2$ in (2) & (3)
$24 a_0+10 a_1=-8$
$6 a_0+5 a_1=-8$
on solving this we get
$a _1=-\frac{12}{5}, a _0=\frac{2}{3}$
$f(x)=\frac{2}{3} x^6-\frac{12}{5} x^5+2 x^4$
$f^{\prime}(x)=4 x^5-12 x^4+8 x^3=4 x^3\left(x^2-3 x+2\right)$
$=4 x^3(x-2)(x-1)$