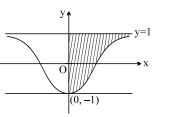
Q. Suppose $f$ is defined from $R \rightarrow[-1,1]$ as $f( x )=\frac{ x ^2-1}{ x ^2+1}$ where $R$ is the set of real number. Then the statement which does not hold is
Application of Integrals
Solution:
$y=f(x)=\frac{x^2-1}{x^2+1}=1-\frac{2}{x^2+1}$
$f^{\prime}(x)=\frac{4 x}{\left(x^2+1\right)^2}$
$x>0$, fis increasing and $x<0$ fis decreasing $\Rightarrow(B)$ is true range is $[-1,1) \Rightarrow$ into $\Rightarrow$ (A) is false;
minimum value occurs at $x=0$ and $f(0)=-1 \Rightarrow$
(C) is false
$A=2 \int\limits_0^{\infty}\left(1-\frac{x^2-1}{x^2+1}\right) d x=4 \int\limits_0^{\infty} \frac{d x}{x^2+1}=\left.4 \cdot \tan ^{-1}\right|_0 ^{\infty}=4 \cdot \frac{\pi}{2}=2 \pi \Rightarrow$(D) is false