Question

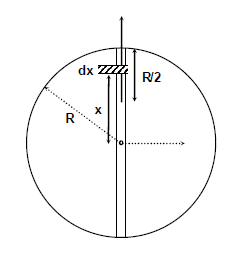
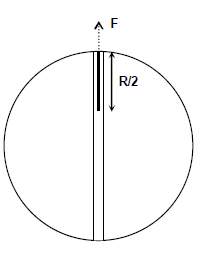
Suppose a frictionless tunnel is made inside the earth along a diameter. A string of mass $m$ and length $R/2$ is suspended in the tunnel with one end of the string at the surface of the earth. A force $F$ is applied to pull the string slowly to the surface to the earth. Find the work done by the force $F$ to pull the string completely on the surface of the earth. (Given acceleration due to gravity on the surface of the earth $=g$ ,, radius of the earth $=R$ )

• A. $\frac{m g R}{2}$
• B. $\frac{3 m g R}{4}$
• C. $\frac{5 m g R}{12}$
• D. $\frac{5 m g R}{24}$

Answer 1

Answer: (D)

$U_{i}=\displaystyle \int \left(\right.dm\left.\right)v=\displaystyle \int _{R / 2}^{R}-\frac{m}{R / 2}d\times \frac{G M}{2 R}\left(3 - \frac{x^{2}}{R^{2}}\right)$
$=\frac{29 G M m}{24 R}=\frac{29 g R^{2} m}{24}=\frac{29 m g R}{24}$
$U_{f}=-\frac{G M m}{R}=-\frac{g R^{2} m}{R}=-mgR$
$W=\Delta U=U_{f}-U_{i}=\frac{5 m g R}{24}$