Q.
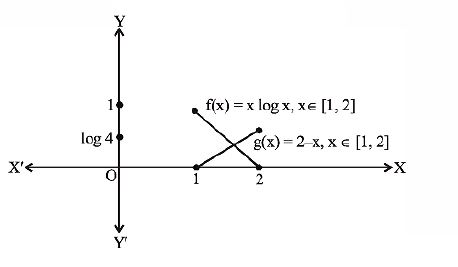
Statement-1 : The equation $x log x = 2 - x$ is satisfied by at least one value of $x$ lying between $1$ and $2$.
Statement-2 : The function $f(x) = x log x$ is an increasing function in $[1,2]$ and $g (x)=2-x$ is a decreasing function in $[1, 2]$ and the graphs represented by these functions intersect at a point in $[1,2]$
Solution:
$f\left(x\right)=x\,log\,x,\,f\left(1\right) = 0,\,f\left(2\right) = 4$
$g\left(x\right) = 2-x,\,g\left(1\right)=1,\,g\left(2\right) = 0$
$log 10 > log\,4 \Rightarrow 1 > log\,4$
Thus statement -1 and 2 both are true and statement-2 is a correct explanation of statement 1.