Q.
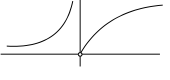
Statement-1: $f ( x )=\tan ^{-1} x$ is a one-one function.
because
Statement-2: If $f ^{\prime}( x )>0$ for all $x$ in domain of $f ( x )$ then $f ( x )$ is one-one..
Inverse Trigonometric Functions
Solution:
$f (x) = \tan x, f ' (x) > 0 $
for all x in the domain of $f$ but tan $x$ is not one-one, it is many one