Q. Solution set of the inequality $\left(\log _2 x\right)^4-\left(\log _{1 / 2} \frac{x^3}{8}\right)^2+9 \log _2\left(\frac{32}{x^2}\right)<4\left(\log _{1 / 2} x\right)^2$ is (a, b) $\cup$ (c, d) then the correct statement is
Continuity and Differentiability
Solution:
$\left(\log _2 x\right)^4-\left(\log _2\left(\frac{x}{2}\right)^3\right)^2+9\left[\log _2 32-\log _2 x^2\right]<4\left(\log _2 x\right)^2 ($ note $x>0)$
$\left(\log _2 x\right)^4-\left(3 \log _2 x-3\right)^2+45-18 \log _2 x<4\left(\log _2 x\right)^2 $
$\text { let } \log _2 x=t$
$t ^4-(3 t -3)^2+45-18 t <4 t ^2 \Rightarrow t ^4-\left(9 t ^2+9-18 t \right)-18 t +45<4 t ^2 $
$\Rightarrow t ^4-13 t ^2+36<0 \Rightarrow \left( t ^2-4\right)\left( t ^2-9\right)<0$
$\Rightarrow 4< t ^2<9$
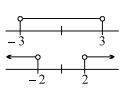
$ t ^2<9 \Rightarrow -3< t <3$
and $t^2>4 \Rightarrow t>2$ or $t<-2$
hence, $t \in(-3,-2) \cup(2,3)$
$x \in\left(\frac{1}{8}, \frac{1}{4}\right) \cup(4,8) \Rightarrow B , C$