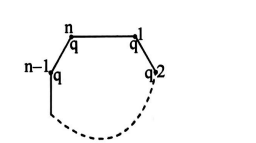
Question

Small identical balls with equal charges are fixed at vertices of regular polygon with side $a$. At a certain instant, one of the balls is released & a sufficiently long time interval later, the ball adjacent to the first released ball is freed. The kinetic energies of the released balls are found to differ by $K$ at a sufficiently long distance from the polygon. Determine the charge $q$ of each ball. If it is $\frac{1}{a} \times 10^{-4} C$. Find $a .( k =10$ Joule, side length $=1 \,m )$

Answer 1

$KE _{1}:$ Kinetic energy of $1^{\text {st }}$
$KE _{2}:$ Kinetic energy of $2^{\text {nd }}$
$K.E_1$
$=\frac{q^{2}}{4 \pi \varepsilon_{0} r_{12}}+\frac{q^{2}}{4 \pi \varepsilon_{0} r_{13}}+\ldots+\frac{q^{2}}{4 \pi \varepsilon_{0} r_{1 n}}$
$K.E_2$
$=\frac{ q ^{2}}{4 \pi \varepsilon_{0} r _{22}}+\frac{ q ^{2}}{4 \pi \varepsilon_{0} r _{23}}+\ldots .+\frac{ q ^{2}}{4 \pi \varepsilon_{0} r _{2 n }}$
$=\frac{ q ^{2}}{4 \pi \varepsilon_{0} r _{1 n }}+\frac{ q ^{2}}{4 \pi \varepsilon_{0} r _{1, n -1}}+\ldots+\frac{ q ^{2}}{4 \pi \varepsilon_{0} r _{13}}$
$K = KE _{1}- KE _{2}=\frac{ q ^{2}}{4 \pi \varepsilon_{0} r _{1 \alpha}}=\frac{ q ^{2}}{4 \pi \varepsilon_{0} a }$
$q=\sqrt{4 \pi \varepsilon_{0} a k}$