Q.
Six $X$ have to be placed in the squares of Figure such that each row contain at least one $X$. The number of ways in which this can be done is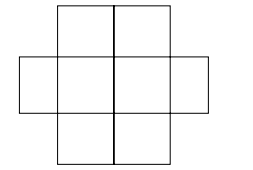
Permutations and Combinations
Solution:
This can be done in four mutually exclusive ways as follows:
Row
$R_1$
Row $R_2$
Row $R_3$
Number of ways
I
1
3
2
$\left({ }^2 C_1\right)\left({ }^4 C_3\right)\left({ }^2 C_2\right)=8$
II
1
4
1
$\left({ }^2 C_1\right)\left({ }^4 C_4\right)\left({ }^2 C_1\right)=4$
III
2
2
2
$\left({ }^2 C_2\right)\left({ }^4 C_2\right)\left({ }^2 C_2\right)=6$
IV
2
3
1
$\left({ }^2 C_2\right)\left({ }^4 C_3\right)\left({ }^2 C_1\right)=8$
Total
26
| Row $R_1$ | Row $R_2$ | Row $R_3$ | Number of ways | |
|---|---|---|---|---|
| I | 1 | 3 | 2 | $\left({ }^2 C_1\right)\left({ }^4 C_3\right)\left({ }^2 C_2\right)=8$ |
| II | 1 | 4 | 1 | $\left({ }^2 C_1\right)\left({ }^4 C_4\right)\left({ }^2 C_1\right)=4$ |
| III | 2 | 2 | 2 | $\left({ }^2 C_2\right)\left({ }^4 C_2\right)\left({ }^2 C_2\right)=6$ |
| IV | 2 | 3 | 1 | $\left({ }^2 C_2\right)\left({ }^4 C_3\right)\left({ }^2 C_1\right)=8$ |
| Total | 26 |