Question

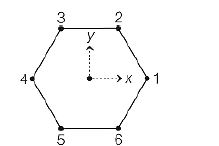
Six objects are placed at the vertices of a regular hexagon. The geometric centre of the hexagon is at the origin with objects 1 and 4 on the $X$-axis (see figurei. The mass of the $k$ th object is $m_{k}=k^{i} M \mid \cos \theta_{k} \|$, where $i$ is an integer, $M$ is a constant with dimension of mass and $\theta_{k}$ is the angular position of the $k$ th vertex measured from the positive $X$-axis in the counter-clockwise sense. If the net gravitational force on a body at the centroid vanishes, the value of $i$ is

• A. 0
• B. 1
• C. 2
• D. 3

Answer 1

Answer: (A)

For a mass m at centroid of hexagon (at origin), net force is zero when
$\Sigma F_{x}=0$ and $\Sigma F_{y}=0$

Now, $\Sigma F_{x}=$ sum of all x-components of forces on m due to masses at vertices of hexagon.
$=\frac{Gm}{r^{2}}\left(\Sigma \left(k^{i}M \cos \theta_{k} \cos \theta_{k\theta}\right)\right)$
$=\frac{G m M}{r^{2}}\left(1^{i}\left|\cos 0^{\circ}\right| \cdot \cos 0^{\circ}+2^{i}\left|\cos 60^{\circ}\right|\right.$
$\cdot \cos 60^{\circ}+3^{i}\left|\cos 120^{\circ}\right| \cdot \cos 120^{\circ}$
$+4^{i}\left|\cos 180^{\circ}\right| \cdot \cos 180^{\circ}$
$+5^{i}\left|\cos 240^{\circ}\right| \cdot \cos 240^{\circ}$
$\left.+6^{i}\left|\cos 300^{\circ}\right| \cdot \cos 300^{\circ}\right)$
$=\frac{G M m}{r^{2}} \cdot\left(1^{i}+\frac{2^{i}}{4}-\frac{3^{i}}{4}-4^{i}-\frac{5^{i}}{4}+\frac{6^{i}}{4}\right)$
As $'\Sigma F_{x} =0,$ for net force on m to be zero, we have
$1^{i}+\frac{2^{i}}{4}-\frac{3^{i}}{4}-4^{i}-\frac{5^{i}}{4}+\frac{6^{i}}{4}=0 $
Above equation is satisfied with $i= 0.$