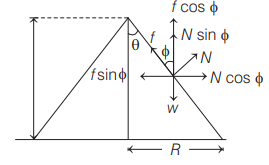
Question

Sand is to be piled up on a horizontal ground in the form of a regular cone of a fixed base of radius $R$. Coefficient of static friction between the sand layers is $\mu .$ Maximum volume of the sand can be piled up in the form of cone without slipping on the ground is

• A. $\frac{\mu R^{3}}{3 \pi}$
• B. $\frac{\mu R^{3}}{3}$
• C. $\frac{\pi R^{3}}{3 \mu}$
• D. $\frac{\mu \pi R^{3}}{3}$

Answer 1

Answer: (D)

Let $h=$ critical height of sand cone of radius $R$
Then, for a sand particle to be in equilibrium (it must no slips to the ground)

$f \sin \phi=N \cos \phi$
where, $f=$ friction, $N=$ normal reaction and $f=\mu N$
$\Rightarrow \mu N \sin \phi=N \cos \phi$
$\Rightarrow \tan \phi=\frac{1}{\mu}=\frac{R}{h}$ (from figure)
So, maximum volume of sand cone that can be formed over level ground is
$V_{\max }=\frac{1}{3} \pi R^{2} h=\frac{1}{3} \pi R^{2}(\mu R)=\frac{\mu \pi R^{3}}{3}$