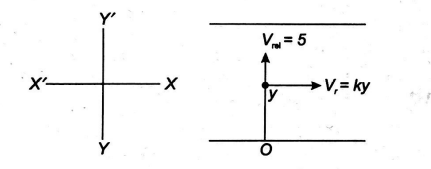
Question

River stream velocity grows in proportion to the distance from the bank and reaches its maximum velocity $2\, ms ^{-1}$ in the middle. Near the bank velocity is zero. The velocity of a swimmer in still water is $5\, ms ^{-1}$ and is directed perpendicular to river stream. The width of river is $100\, m$. The drifting in swimmer is $5 \,n$ meter. The value of $n$ is _____.

Answer 1

$v_{x}=k y$ and $v_{y}=5$

$\therefore y=5 t, $ At middle point, $ 50=5 t$
$\therefore t=10 \,s$
$ \because v_{x}=k y $
At middle, $v_{x}=2 $
$ \therefore k=\frac{2}{50} $
$ \therefore v_{x}=\frac{2}{50} y=\frac{y}{25}=\frac{5 t}{25}=\frac{t}{5}$
$\Rightarrow \frac{d x}{d t}=\frac{t}{5} $
$ \therefore \int\limits_{0}^{x_{0}} d x=\int\limits_{0}^{10} \frac{t}{5} d t$
$ \therefore x_{0}=10 \,m $ up to middle
$\therefore$ Total drifting $=2 \times 10=20\, m$
$\therefore n=4$