Question

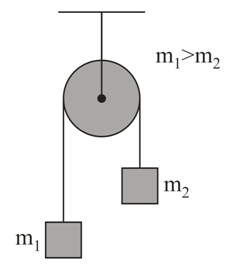
Pulley of atwood machine has mass $m_{1}$ and is free to rotate about its geometrical center without friction. Centre of mass of the pulley is at a distance $R/2$ from geometrical centre, where $R$ is the radius of the pulley. There is no slipping between the string and pulley. The ratio of maximum acceleration to minimum acceleration of block of mass $m_{1}$ is (Take $m_{1}R^{2}$ as moment of inertia of pulley about axis of rotation, $\frac{m_{1}}{ m_{2}}=3$ )

Answer 1

$m_{1}g-T_{1}=m_{1}a$ .......(i)
$T_{2}-m_{2}g=m_{2}a$ ....(ii)
$T_{1}-T_{2}\pm\frac{m_{1} g}{2}=m_{1}a$
$\left(m_{1} - m_{2}\right)g\pm\frac{m_{1} g}{2}=\left(2 m_{1} + m_{2}\right)a$
$a=\frac{2 m_{2} g \pm \frac{3 g m_{2}}{2}}{7 m_{2}}$
$a_{max}=\frac{g}{2}$
$a_{min}=\frac{g}{14}$
$\frac{a_{max}}{a_{min}}=7$