Q.
Pressure versus temperature graph of an ideal gas is shown, The density of gas at point $A$ is $\rho _{0}$ then the density of gas at point $B$ would be
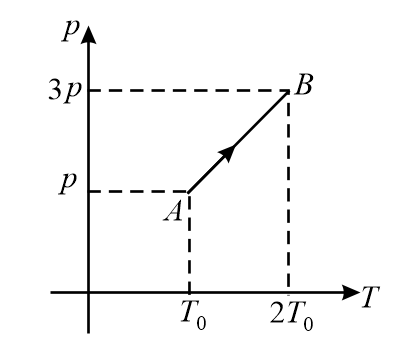
NTA AbhyasNTA Abhyas 2022
Solution: