Q.
$PQRS$ is a square loop of a conducting wire. A current $I$ enters the loop at $P$ and leaves the loop at $S .$ The magnitude of magnetic field at the centre $O$ of the square is
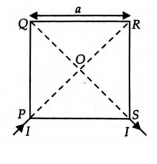
Moving Charges and Magnetism
Solution:
