Q.
Point masses $ m_1 $ and $m_2 $ are placed at the opposite ends of a rigid rod of length $L$, and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point $P$ on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity $ \omega_0$ is minimum, is given by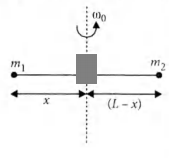
AIPMTAIPMT 2015System of Particles and Rotational Motion
Solution:
