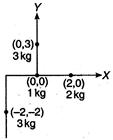
Q. Point masses $1,2,-3$ and $4\, kg$ are lying at the point $(0,0,0)(2,0,0)$ $(0,3,0)$ and $(-2,-2,0)$ respectively. The moment of inertia of this system about $x$-axis will be
J & K CETJ & K CET 2004
Solution:
Moment of inertia of the whole system about the axis of rotation will be equal to the sum of the moments of inertia of all the particles,
$I=I_{1}+I_{2}+I_{3}+I_{4}$
$\therefore I=m_{1} r_{1}^{2}+m_{2} r_{2}^{2}+m_{3} r_{3}^{2}+m_{4} r_{4}^{2}$
$I=(1 \times 0)+(2 \times 0)+\left(3 \times 3^{2}\right)+4(-2)^{2}$
$I=0+0+27 +16=43\, kg -m^{2}$