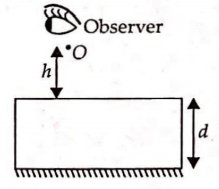
Question

point luminous object (O) is at a distance h from front face of a glass slab of width d and of refractive index p. On the back face of slab is a reflecting plane mirror. An observer sees the image of object in mirror as shown in figure. Distance of image from front face as seen by observer will be

• A. $h+\frac{2d}{\mu}$
• B. $2h+2d$
• C. $h+d$
• D. $h+ \frac{d}{\mu}$

Answer 1

Answer: (A)

As shown in figure glass slab will form the image of bottom i.e.y mirror $M M'$ at a depth $(\frac{d}{\mu})$ from its front face. So the distance of object $O$ from virtual mirror $mm'$ will be $h +(\frac{d}{\mu})$.
Now as a plane mirror forms image behind the mirror at the same distance as the object is in front of it, the distance of image $I$ from mm will be $h+(\frac{d}{\mu})$ and as the distance of virtual mirror from the front face of slab is $(\frac{d}{\mu})$, the distance of image $I$ from front face as seen by
observer $= [h+\frac{d}{\mu}] + \frac{d}{\mu} $
$= h+\frac{2d}{\mu}$