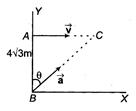
Question

Particle $A$ moves along the line $ y=4\sqrt{3}\,m $ with constant velocity v of magnitude $2.0 \,m/s$ and directed parallel to the positive $x$ -axis (see figure). Particle $B$ starts at the origin with zero speed and constant accelerationa (of magnitude $ 4.0\,m/s^{2} $ ) at the same instant that the particle A passes the y axis. The angle $ \theta $ between a and the positive $y$ axis that would result in a collision between these two particles should have a value equal to

• A. $ 30^{\circ} $
• B. $ 45^{\circ} $
• C. $ 50^{\circ} $
• D. $ 60^{\circ} $

Answer 1

Answer: (A)

Given that $y=4 \sqrt{3} m$
For particle $A$, $v =2\, m / s$
and For particle $B\, a=4 \,m / s ^{2}$
Let particle are collide after $t\, sec$.
distance covered by $A$ in $t \,sec .=2 t$
and $B ,=\frac{1}{2} \times 4 \times t^{2}$
For collision $2 t=\frac{1}{2} \times 4 \times t^{2}$
$t=1 \,sec$.
Velocity of $B=4 \times 1=4\, m / s$
Now, from $MBC \sin \theta=\frac{2}{4}=\frac{1}{2} $
$\theta=30^{\circ}$