Q.
Parallel beam containing light of $\lambda=400 \,nm$ and $500 \,nm$ is incident on a prism as shown in figure. The refractive index $\mu$ of the prism is given by the relation,
$\mu(\lambda)=1.20+\frac{0.8 \times 10^{-14}}{\lambda^{2}}$
Which of the following statement is correct?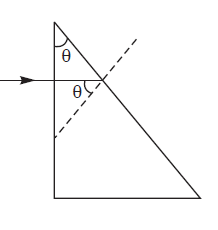
Ray Optics and Optical Instruments
Solution:
