Q.
PARAGRAPH "X"
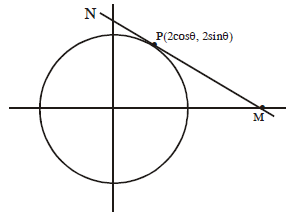
Let $S$ be the circle in the $xy$-plane defined by the equation $x^2 + y^2 = 4$.
Question: Let $P$ be a point on the circle $S$ with both coordinates being positive. Let the tangent to $S$ to $P$ intersect the coordinate axes at the points $M$ and $N$. Then, the mid-point of the line
segment $MN$ must lie on the curve
JEE AdvancedJEE Advanced 2018
Solution:
Tangent at $P(2 \cos \theta, 2 \sin \theta)$ is $x \cos \theta + y \sin \theta = 2$
$M(2 \sec \theta , 0)$ and $N(0, 2 cosec \theta)$
Let midpoint be (h, k)
$h = \sec \theta , k = cosec \theta$
$\frac{1}{h^2} + \frac{1}{k^2} = 1$
$\frac{1}{x^2} + \frac{1}{y^2} = 1 $