Q.
PARAGRAPH 1
Consider a simple RC circuit as shown in Figure 1 .
Process 1: In the circuit the switch $S$ is closed at $t =0$ and the capacitor is fully charged to voltage $V _{0}$ (i.e. charging continues for time $T \gg RC$ ). In the process some dissipation $\left( E _{ D }\right)$ occurs across the resistance $R$. The amount of energy finally stored in the fully charged capacitor is $E_{C}$.
Process 2: In a different process the voltage is first set to $\frac{ V _{0}}{3}$ and maintained for a charging time $T \gg RC$. Then the voltage is raised to $\frac{2 V _{0}}{3}$ without discharging the capacitor and again maintained for time $T \gg RC$. The process is repeated one more time by raising the voltage to $V _{0}$ and the capacitor is charged to the same final
voltage $V _{ o }$ as in Process 1 .
These two processes are depicted in Figure 2 .
In Process 2, total energy dissipated across the resistance $E_{D}$ is: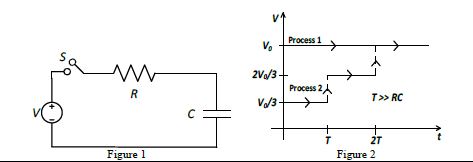
JEE AdvancedJEE Advanced 2017
Solution: