Question

$P(r)$ is magnitude of physical quantity as a function of $r$ (distance from centre of spherical distribution of radius $R$). Match the following columns and select the correct option from the codes given below.

Column-I		column-II
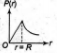
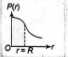
i.		p.	p(r) is variation of gravitational potential for a uniform volumrtric spherical distribution of mass.
ii.		q.	p(r) is variation of gravitational potential for a uniform spherical shell
iii.		r.	p(r) is variation of gravitational field intensity for a uniform volumetric spherical distribution of mass
iv.		s.	p(r) is variation of gravitational field intensity for a uniform spherical shell.

• A. (i) - (s) , (ii)- (r), (iii)-(q), (iv) - (p)
• B. (i) - (q), (ii) - (s), (iii) - (r), (iv) - (p)
• C. (i) - (q), (ii) - (r), (iii) - (s), (iv) - (p)
• D. (i) - (r), (ii) - (s), (iii) - (p), (iv) - (q)

Answer 1

Answer: (C)

Potential sphere $V = -\frac{GM}{2R^3}(3R^2 - r^2)$ for $r \le R$
$V = -\frac{GM}{r}$ for $r > R$
Shell $V = -\frac{GM}{R}$ for $r \le R$
$V = -\frac{GM}{r} $ for $r > R$
Field sphere $E_g = \frac{GM}{R^3} .r$ for $r \le R$
$E_g = \frac{GM}{r^2}$ for $r > R$
Shell $E_g = $ zero for $r < R$
$E_g = \frac{GM}{r^2}$ for $r \ge R$