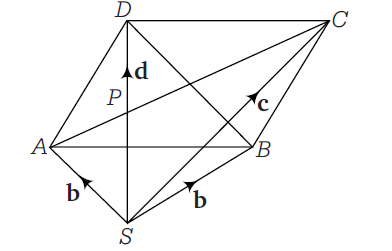
Question

$P$ is the point of intersection of the diagonals of the parallelogram $A B C D$. If $S$ is any point in space and $S A + S B + S C + S D =\lambda S P$, then $\lambda$ equals

• A. 2
• B. 4
• C. 6
• D. 8

Answer 1

Answer: (B)

Taking $S$ as origin, let the position vectors of $A, B$,
$C$ and $D$ be $a , b , c$ and $d$ respectively.
In $\Delta S A C$, $P$ is the mid-point of $A C$.
$\therefore SA + SC =2 SP \ldots( i )$

In $\Delta S B D, P$ is the mid-point of $B C$.
$\therefore $ $SB + SD =2 SP \,......(ii)$
On adding Eqs. (i) and (ii), we get
$SA + SB + SC + SD =4 SP$
But it is given, $SA + SB + SC + SD =\lambda SP$
On comparing, we get $\lambda=4$