Q.
Six $X$ 's have to be placed in the square of the figure such that each row contains atleast one ' $X$ '. In how many different ways can this be done?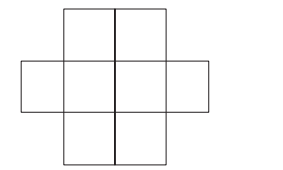
Permutations and Combinations
Solution: