Q.
One plano-convex and one plano-concave lens of same radius of curvature $'R'$ but of different materials are joined side by side as shown in the figure. If the refractive index of the material of $1$ is $\mu_1$ and that of $2$ is $\mu_2$, then the focal length of the combination is :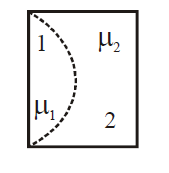
Solution: