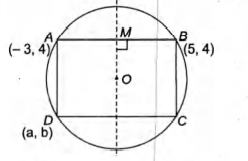
Question

One of the diameters of the circle circumscribing the rectangle $ABCD\, 4y = x + 7$. If $A$ and $B$ are the points $(-3, 4)$ and $(5, 4)$ respectively, then find the area of rectangle.

Answer 1

Let $O$ be the centre of circle and $M$ be mid-point of $AB$.

Then, $ OM\perp AB \Rightarrow M(1,4)$
Since, slope of $A B = 0 $
Equation of straight line $MO$ is $x = 1$ and equation of diameter is $4y = x + 7$.
$\Rightarrow$ Centre is $(1, 2).$
Also, $O$ is mid-point of $BD$
$\Rightarrow \Bigg(\frac{\alpha+5}{2},\frac{\beta+4}{2}\Bigg)= (1,2) \Rightarrow \alpha=-3,\beta=0$
$\therefore AD=\sqrt{(-3 + 3)^2+(4 - 0)^2}=4$
and $ AB=\sqrt{64+0}=8$
Thus, area of rectangle $= 8 \times 4 = 32$ sq units