Question

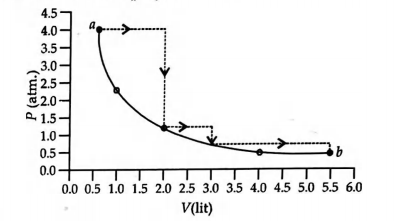
One mole of an ideal gas is taken from $a$ to $b$ along two paths denoted by the solid and the dashed lines as shown in the graph below. If the work done along the solid line path is $w_{s}$ and that along the dotted line path is $w_{d}$, the integer closest to the ratio $w_{d}/w_{s}$ is

• A. $2$
• B. $0$
• C. $4$
• D. none of these

Answer 1

Answer: (A)

Solid line path work done $(w_{s})$ is isothermal because PV is constant (Boyles law) and dashed line (horizontal) path work done $w_{d}$ is isobaric. Work done in vertical line is zero as
$\Delta\,V =0$
Total work done on solid line path $(w_{s})=2.303\,nRT\,log\,\frac{V_{2}}{V_{1}}$
$=2.303\,PV\,log \frac{V_{2}}{V_{1}}=2.303\times 4\times 0.5\,log \frac{5.5}{0.5}=4.8\,L\,atm$
Total work done on dashed line path ${(w_{d})}= P \Delta\,V$
$=4 \times (2-0.5)+1(3-2)+0.5(5.5-3)=6+1+1.25=8.25$
so, $\frac{w_{d}}{w_{s}}=\frac{8.25}{4.8}=2 \approx 1.72$