Q.
One end of a spring of negligible unstretched length and spring constant $k$ is fixed at the origin $(0,0)$. a point particle of mass $m$ carrying a positive charge $q$ is attached at its other end. The entire system is kept on a smooth horizontal surface. When a point dipole $\vec{p}$ pointing towards the charge $q$ is fixed at the origin, the spring gets stretched to a length I and attains a new equilibrium position (see figure below). If the point mass is now displaced slightly by $\Delta l < < l$ from its equilibrium position and released, it is found to oscillate at frequency $\frac{1}{\delta} \sqrt{\frac{k}{m}}$. The value of $\delta$ is ______.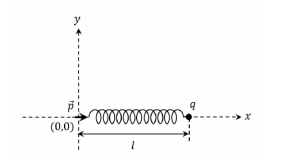
JEE AdvancedJEE Advanced 2020
Solution:
