Q.
One end of a spring of negligible unstretched length and spring constant $k$ is fixed at the origin $\left(\right.0,0\left.\right)$ A point particle of mass m carrying a positive charge $q$ is attached at its other end. The entire system is kept on a smooth horizontal surface. When a point dipole $\vec{p}$ pointing towards the charge $q$ is fixed at the origin, the spring gets stretched to a length I and attains a new equilibrium position (see figure below). If the point mass is now displaced slightly by $\Delta \left|\right.\ll\left|\right.$ from its equilibrium position and released, it is found to oscillate at frequency $\frac{\delta \pi }{1}\sqrt{\frac{k}{m}}.$ The value of $\delta$ is
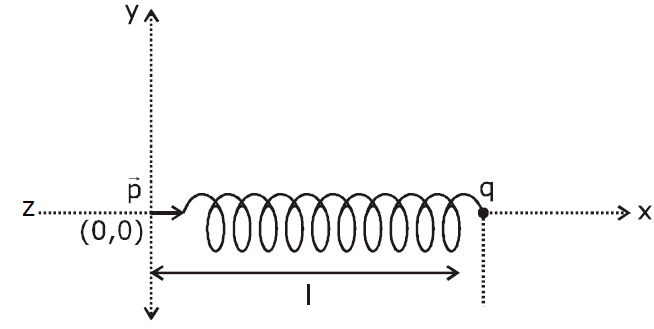
NTA AbhyasNTA Abhyas 2022
Solution:
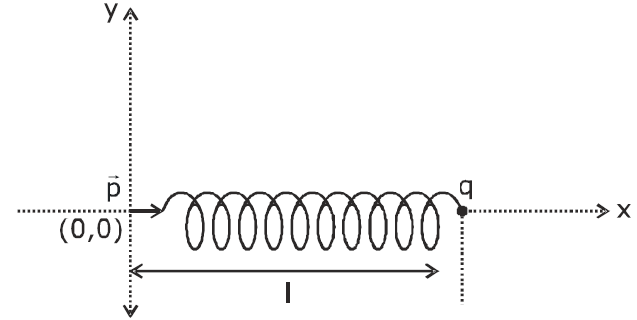
 $U=\frac{1}{2} kx ^{2}+\frac{p \times q}{4 \pi \epsilon_{0} x ^{2}} \ldots . .$ (i)
$U=\frac{1}{2} kx ^{2}+\frac{p \times q}{4 \pi \epsilon_{0} x ^{2}} \ldots . .$ (i)