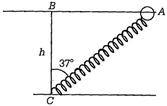
Q. One end of a spring of natural length h and spring constant k is fixed at the ground and the other is fitted with a smooth ring of mass m which is allowed to slide on a horizontal rod fixed at a height h. Initially, the spring makes an angle $ 37{}^\circ $ with the vertical when the system is released from the rest. The speed of the ring, when the spring becomes vertical will be
CMC MedicalCMC Medical 2015
Solution:
Consider the situational diagram
Here, $ \theta =37{}^\circ , $ $ l=h= $ natural length of spring Also, let the velocity be v. From the diagram $ \cos \,37{}^\circ =\frac{BC}{AC}\Rightarrow \frac{4}{5}=0.8=\frac{h}{h+x} $ $ \therefore $ $ AC=h+x=\frac{5h}{4}\Rightarrow x=\frac{h}{4} $ Applying work-energy theorem, $ \frac{1}{2}k\,{{x}^{2}}=\frac{1}{2}m{{v}^{2}}\Rightarrow v=x\sqrt{\frac{k}{m}} $ $ \Rightarrow $ $ v=\frac{h}{4}\sqrt{\frac{k}{m}} $