Q.
On an inclined plane of inclination $\alpha =30^\circ $ with respect to the horizontal, a particle is projected with a speed $u=2ms^{- 1}$ from the base of the plane making an angle $\theta =15^\circ $ with respect to the plane as shown in the figure. The distance from the base at which the particle hits the plane is close to:
(Take $g=10ms^{- 2}$ )
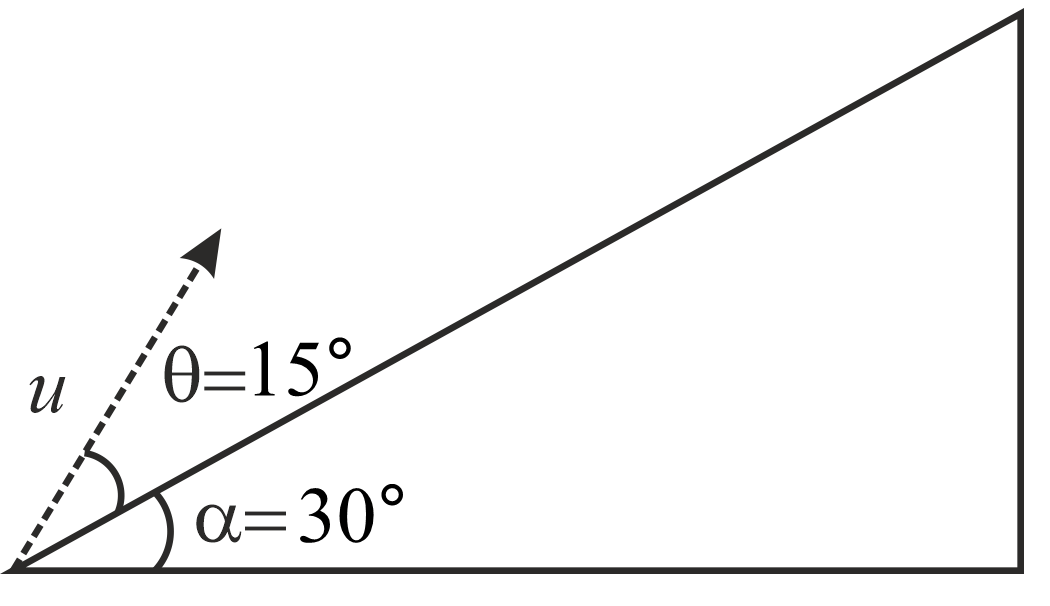
NTA AbhyasNTA Abhyas 2020
Solution: