Q.
On a frictionless horizontal surface, assumed to be the $x-y$ plane, a small trolley $A$ is moving along a straight line parallel to the $x-axis$ (see figure) with a constant velocity of $(\sqrt 3 - 1)m/s.$.
At a particular instant when the line OA makes an angle of $45^{\circ}$ with the $x$-axis, a ball is thrown along the surface from the origin $O$.
Its velocity makes an angle $\varnothing$ with the x-axis and it hits the trolley.
(a) The motion of the ball is observed from the frame of the trolley.
Calculate the angle $\theta$ made by the velocity vector of the ball with the $x$-axis in this frame.
(b) Find the speed of the ball with respect to the surface, if $\varnothing = 4\theta / 3.$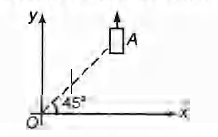
IIT JEEIIT JEE 2002
Solution: