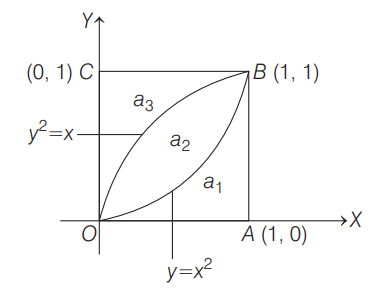Question

$O A B C$ is a unit square where $O$ is the origin and $B=(1,1)$. The curves $y^{2}=x$ and $x^{2}=y$ divide the area of the square into three parts $OABO, O B O$ and $O B C O$. If $a_{1}, a_{2}, a_{3}$ are the areas (in sq units) of these parts respectively, then $a_{1}+2 a_{2}+3 a_{3}=$

• A. 1
• B. 2
• C. 6
• D. 64

Answer 1

Answer: (B)

$\because a_{1}+a_{2}+a_{3}=1$ ...(i)
and due to symmetry $a_{1}=a_{3}$ ...(ii)
Now, $a_{2} =\int\limits_{0}^{1}\left(\sqrt{x}-x^{2}\right) d x$
$=\left[\frac{2}{3} x^{3 / 2}-\frac{x^{3}}{3}\right]_{0}^{1}=\frac{2}{3}-\frac{1}{3}=\frac{1}{3}$

So, $a_{1}+a_{3}+\frac{1}{3}=1$
$\Rightarrow a_{1}+a_{3}=\frac{2}{3}$ ...(iii)
From Eqs. (ii) and (iii),
$a_{1}=a_{3}=\frac{1}{3}=a_{2}$
So, $a_{1}+2 a_{2}+3 a_{3}=\frac{1}{3}+\frac{2}{3}+\frac{3}{3}=2$