Q.
Number of ways in which the letters of the word "NATION" can be
filled in the given figure such that no row remains empty and each box
contain not more than one letter is $(K)6!$. The value of K equals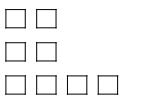
Permutations and Combinations
Solution: