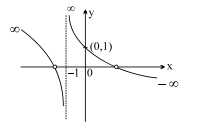
Q. Number of roots of the function $f( x )=\frac{1}{( x +1)^3}-3 x +\sin x$ is
Application of Derivatives
Solution:
$ f^{\prime}(x)=-\frac{3}{(x+1)^4}-3+\cos x<0$
hence $f(x)$ is always decreasing, Also as $x \rightarrow \infty, f(x) \rightarrow-\infty$ and as $x \rightarrow-\infty, f(x) \rightarrow+\infty$ hence one positive and one negative root
Graph is as shown