Question

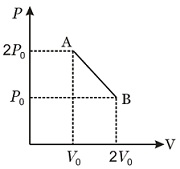
$n$ moles of an ideal gas undergoes a process $A \rightarrow B$ as shown in the diagram. The maximum temperature of the gas during the process is

• A. $\frac{3 \text{P}_{0} \text{V}_{0}}{2 \textit{nR}}$
• B. $\frac{9 \text{P}_{0} \text{V}_{0}}{4 \textit{nR}}$
• C. $\frac{9 \text{P}_{0} \text{V}_{0}}{2 \textit{nR}}$
• D. $\frac{9 \text{P}_{0} \text{V}_{0}}{\textit{nR}}$

Answer 1

Answer: (B)

Since the P-V graph of the process is a straight line and two points (V₀, 2P₀) and (2V₀, P₀) are known, its equation will be
$\left(\textit{P} - \left(\text{P}\right)_{0}\right)=\frac{\left(2 \left(\text{P}\right)_{0} - \left(\text{P}\right)_{0}\right)}{\left(\left(\text{V}\right)_{0} - 2 \left(\text{V}\right)_{0}\right)}\left(\textit{V} - 2 \left(\text{V}\right)_{0}\right)=\frac{\left(\text{P}\right)_{0}}{\left(\text{V}\right)_{0}}\left(2 \left(\text{V}\right)_{0} - \textit{V}\right)$
$∴ \, \, \textit{P}=3\text{P}_{0}-\frac{\text{P}_{0} \textit{V}}{\text{V}_{0}}$
According to the equation for an ideal gas,
$\textit{T}=\frac{\textit{pV}}{\textit{nR}}$
$=\left(3 \left(\text{P}\right)_{0} - \frac{\left(\text{P}\right)_{0} \textit{V}}{\left(\text{V}\right)_{0}}\right)\frac{\textit{V}}{\textit{nR}}$
$=\frac{3 \text{P}_{0} \text{V}_{0} \textit{V} - \text{P}_{0} \textit{V}^{2}}{\textit{nR} \text{V}_{0}}$ ...(i)
For $T$ to maximum, $\frac{\textit{dT}}{\textit{dV}}=0$
$3\text{P}_{0}\text{V}_{0}-2\text{P}_{0}\textit{V}=0$
or $\textit{V}=\frac{3 \text{V}_{0}}{2}$ ...(ii)
Putting this value in Eq. (i), we get
$\left(\textit{T}\right)_{\text{max}}=\frac{3 \left(\text{P}\right)_{0} \left(\text{V}\right)_{0} \left(\frac{3 \left(\text{V}\right)_{0}}{2}\right) - \left(\text{P}\right)_{0} \left(\frac{9}{4} \text{V}_{0}^{2}\right)}{\textit{nR} \left(\text{V}\right)_{0}}=\frac{9 \left(\text{P}\right)_{0} \left(\text{V}\right)_{0}}{4 \textit{nR}}$