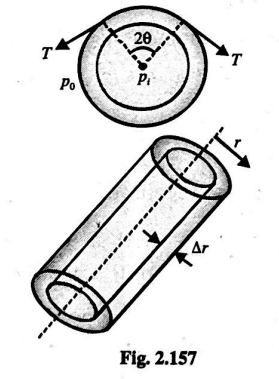
Question

Maximum excess pressure inside a thin-walled steel tube of radius $r$ and thickness $\Delta r(< < r)$, so that the tube would not rupture would be (breaking stress of steel is $\sigma_{\max }$ )

• A. $\sigma_{\max } \times \frac{r}{\Delta r}$
• B. $\sigma_{\max } \times \frac{\Delta r}{r}$
• C. $\sigma_{\max }$
• D. $\sigma_{\max } \times \frac{\Delta 2 r}{r}$

Answer 1

Answer: (B)

Consider a small element of the tube.
$2 T \sin \theta=\Delta p \times A$
where $\Delta p=p_{i}-p_{0}$ and $A$ is the area of element.
As $\theta$ is very small, $\sin \theta \approx \theta$
so, $2 T \times \theta=\Delta p \times l \times(2 r \theta)$

$\Rightarrow \Delta p=\frac{T}{l r} \sigma$ (stress developed in tube)
$=\frac{\Delta T}{\Delta r \times l}$ where $\Delta r \times i$ is the cross-sectional area.
$\sigma=\frac{\Delta p \times l r}{\Delta r \times l}=\Delta p \times \frac{r}{\Delta r}$
For no rupturing, $\sigma \leq \sigma_{\max }$
So, $\Delta p \times \frac{r}{\Delta r} \leq \sigma_{\max }$
$\Delta p(\max , \text { value })=\sigma_{\max } \times \frac{\Delta r}{r}$