Question

Math List I with List II

List I (Current configuration)		List II(Magnetic field at point O)
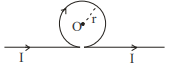
A		I	$B _0=\frac{\mu_0 I }{4 \pi r }[\pi+2]$
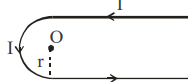
B		II	$B _0=\frac{\mu_0}{4} \frac{ I }{ r }$
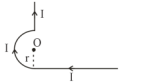
C		III	$B _0=\frac{\mu_0 I }{2 \pi r }[\pi-1]$
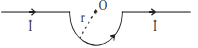
D		IV	$B _0=\frac{\mu_0 I }{4 \pi r }[\pi+1]$

Choose the correct answer from the option given below:

• A. A-III, B-IV, C-I, D-II
• B. A-I, B-III, C-IV, D-II
• C. A-III, B-I, C-IV, D-II
• D. A-II, B-I, C-IV, D-III

Answer 1

Answer: (C)

(A)
$B _{ ab }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } $ (out of the plane)
$ B _{ bcd }=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(2 \pi) $ (in the plane)
$ B _{ de }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } $ (out of the plane)
Hence magnetic field at $O$ is
$B _0=-\frac{\mu_0}{4 \pi} \frac{ I }{ r }+\frac{\mu_0}{4 \pi} \frac{ I }{ r }(2 \pi)-\frac{\mu_0}{4 \pi} \frac{ I }{ r } $
$B _0=\frac{\mu_0}{2 \pi} \frac{ I }{ r }(\pi-1) \ldots \ldots . . \text { (III) }$

$ B _{ ab }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } $ (out of the plane)
$ B _{ bcd }=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi) $ (out of the plane)
$ B _{ de }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } $ (out of the plane)
Hence magnetic field at $O$ is
$ B _0=\frac{\mu_0}{4 \pi} \frac{ I }{ r }+\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi)+\frac{\mu_0}{4 \pi} \frac{ I }{ r }$
$ B _0=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi+2) \ldots \text { (I) }$

$B _{ ab }=\frac{\mu_0}{4 \pi} \frac{I}{ r } $ (in the plane)
$ B _{ bcd }=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi) $ (in the plane)
$ B _{ de }=0 $ (at the axis)
Hence magnetic field at $O$ is
$B _0=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(1+\pi) \ldots \text { (IV) }$

$B _{ ab }=0$ (at the axis)
$B _{ bcd }=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi)$ (out of the plane)
$B _{ de }=0$ (at the axis)
Hence magnetic field at $O$ is
$B _0=\frac{\mu_0 I }{4 r } \ldots$