Q.
List I describes four systems, each with two particles $A$ and $B$ in relative motion as shown in figure.
List II gives possible magnitudes of then relative velocities (in $ms ^{-1}$ ) at time $t=\frac{\pi}{3} s$.
List I
List II
I
$A$ and $B$ are moving on a horizontal circle of radius $1 m$ with uniform angular speed $\omega=1 rad s ^{-1}$. The initial angular positions of $A$ and $B$ at time $t=0$ are $\theta=0$ and $\theta=\frac{\pi}{2}$ respectively. 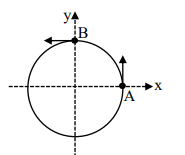
P
$\frac{\sqrt{3}+1}{2}$
II
Projectiles $A$ and $B$ are fired (in the same vertical plane) at $t=0$ and $t=0.1 s$ respectively, with the same speed $v=\frac{5 \pi}{\sqrt{2}} ms ^{-1}$ and at $45^{\circ}$ from the horizontal plane. The initial separation between $A$ and $B$ is large enough so that they do not collide, $\left(g=10 m s ^{-2}\right)$.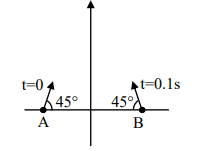
Q
$\frac{(\sqrt{3}-1)}{\sqrt{2}}$
III
Two harmonic oscillators $A$ and $B$ moving in the $x$ direction according to $x_A=x_0 \sin \frac{t}{t_0}$ and $x_B=x_0 \sin \left(\frac{t}{t_0}+\frac{\pi}{2}\right)$ respectively, starting from $t=0$. Take $x_0=1 m , t_0=1 s$.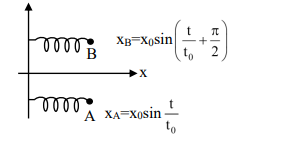
R
$\sqrt{10}$
IV
Particle $A$ is rotating in a horizontal circular path of radius $1 m$ on the $x y$ plane, with constant angular speed $\omega=1 rad s ^{-1}$. Particle $B$ is moving up at a constant speed $3 m s ^{-1}$ in the vertical direction as shown in the figure. (Ignore gravity.)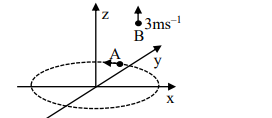
S
$\sqrt{2}$
T
$\sqrt{25 \pi^2+1}$
Which one of the following options is correct?
| List I | List II | ||
|---|---|---|---|
| I | $A$ and $B$ are moving on a horizontal circle of radius $1 m$ with uniform angular speed $\omega=1 rad s ^{-1}$. The initial angular positions of $A$ and $B$ at time $t=0$ are $\theta=0$ and $\theta=\frac{\pi}{2}$ respectively.  |
P | $\frac{\sqrt{3}+1}{2}$ |
| II | Projectiles $A$ and $B$ are fired (in the same vertical plane) at $t=0$ and $t=0.1 s$ respectively, with the same speed $v=\frac{5 \pi}{\sqrt{2}} ms ^{-1}$ and at $45^{\circ}$ from the horizontal plane. The initial separation between $A$ and $B$ is large enough so that they do not collide, $\left(g=10 m s ^{-2}\right)$. |
Q | $\frac{(\sqrt{3}-1)}{\sqrt{2}}$ |
| III | Two harmonic oscillators $A$ and $B$ moving in the $x$ direction according to $x_A=x_0 \sin \frac{t}{t_0}$ and $x_B=x_0 \sin \left(\frac{t}{t_0}+\frac{\pi}{2}\right)$ respectively, starting from $t=0$. Take $x_0=1 m , t_0=1 s$.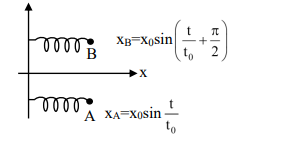 |
R | $\sqrt{10}$ |
| IV | Particle $A$ is rotating in a horizontal circular path of radius $1 m$ on the $x y$ plane, with constant angular speed $\omega=1 rad s ^{-1}$. Particle $B$ is moving up at a constant speed $3 m s ^{-1}$ in the vertical direction as shown in the figure. (Ignore gravity.) |
S | $\sqrt{2}$ |
| T | $\sqrt{25 \pi^2+1}$ | ||
JEE AdvancedJEE Advanced 2022
Solution: