1. Tardigrade
  2. Question
  3. Mathematics
  4. Let z1, z2, z3 represent vertices of triangle A B C and |z1|=|z2|=|z3|. If arg ((z3-z1/z2-z1))=(π/6), then

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

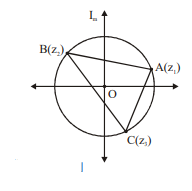
Q. Let $z_1, z_2, z_3$ represent vertices of triangle $A B C$ and $\left|z_1\right|=\left|z_2\right|=\left|z_3\right|$. If $\arg \left(\frac{z_3-z_1}{z_2-z_1}\right)=\frac{\pi}{6}$, then

Complex Numbers and Quadratic Equations

Solution:

From given information, $z _1, z _2, z _3$ lie on circumference of circle whose.
circum-centre is at origin. If its centroid is also at origin then its orthocentre
image
will coincide with its centroid. Hence in this case triangle will be an equilateral.
$\because \arg \left(\frac{ z _1}{ z _2}\right)=-\arg \left(\frac{ z _2}{ z _1}\right)$
Hence option (B) is justified Again apply rotation theorem on $\triangle B O C$, we get $\arg \left(\frac{ z _3}{ z _2}\right)=\frac{\pi}{3} \Rightarrow \arg \left(\frac{ z _2}{ z _3}\right)=-\frac{\pi}{3}$