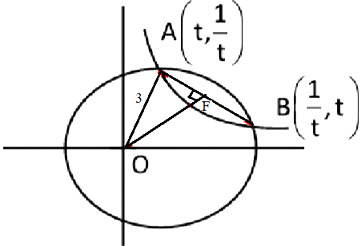
Question

Let $x^{2}+y^{2}=r^{2}$ and $xy=1$ intersect at $A$ and $B$ in the first quadrant. If $AB=\sqrt{14}$ units, then the square of the distance of $AB$ from the origin is equal to

Answer 1

Let, $A=\left(t , \frac{1}{t}\right)$ and $B=\left(\frac{1}{t} , t\right)$ { $\because $ both curves are symmetric about line $y=x$ }
Then, $\left(A B\right)^{2}=\left(t - \frac{1}{t}\right)^{2}+\left(\frac{1}{t} - t\right)^{2}=14$
$\Rightarrow 2\left(t^{2} + \frac{1}{t^{2}}\right)=14+4\Rightarrow t^{2}+\frac{1}{t^{2}}=9$
Now, $\left(O A\right)^{2}=t^{2}+\frac{1}{t^{2}}=9\Rightarrow r^{2}=9$
$\Rightarrow r=3$
$\Rightarrow OF^{2}=9-\frac{14}{4}=5.5$