Q. Let $\vec{a},$ $\vec{b}$ & $\vec{c }$ be non-coplanar unit vectors equally inclined to one another at an acute angle $\theta$ . Then $\left|\left[\vec{a}\, \vec{b}\, \vec{c}\right]\right|$ in terms of $\theta$ is equal to
Vector Algebra
Solution:
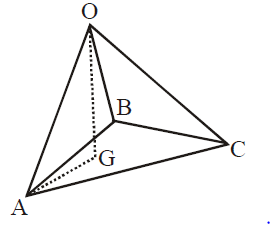
$\overrightarrow{OA}=\vec{a,\,} \overrightarrow{OB}=\vec{b} \,\&\, \overrightarrow{OC}=\vec{c}$ are unit vectors and equally inclined to each other at an acute angle $\theta$.
$\therefore \,$ ABC is an equilateral triangle
$and \, AB=\sqrt{OA^{2}+OB^{2}-2\,OA.\,OB\,cos\,\theta}$
$=\sqrt{2-2\,cos\,\theta}=\sqrt{2}\sqrt{1-cos\,\theta}$
$\therefore \, Area \, of \, \Delta \, ABC, $
$=\frac{\sqrt{3}}{4} AB^{2}=\frac{\sqrt{3}}{4}\cdot2\left(1-cos\,\theta\right)=\frac{\sqrt{3}}{2}\left(1-cos\,\theta\right)$
If G is the centroid of the $\Delta$ ABC, then
$OG \quad=\frac{1}{3} \left|\vec{a} \,+\vec{b}\,+\vec{c}\right|$
$=\frac{1}{3}\sqrt{a^{2}+b^{2}+c^{2}+2\,\vec{a.}\,\vec{b}+2\,\vec{b}.\,\vec{c}+2\,\vec{c.}\,\vec{a}}$
$=\frac{1}{\sqrt{3}} \sqrt{1+2\,cos\,\theta}$
$\therefore \quad\left[\vec{a}\,\vec{b}\, \vec{c}\right]=$ Volume of parallelopiped
$=OG\times2 ar \left(\Delta\,ABC\right)$
$2. \frac{1}{\sqrt{3}} \sqrt{1+2\,cos\,\theta}\times\frac{\sqrt{3}}{2}\left(1-cos\,\theta\right)$
$=\left(1-cos\,\theta\right)\sqrt{1+2\,cos\,\theta}$