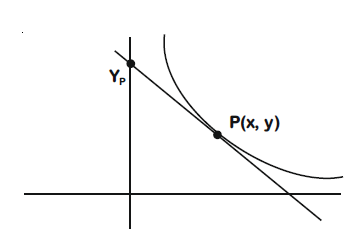
Q. Let $\varGamma$ denote a curve $y = y(x)$ which is in the first quadrant and let the point (1,0) lie on it. Let the tangent to $\varGamma$ at a point P intersect the $y$-axis at $Y_P$. If $PY_P$ has length 1 for each point $P$ on $\varGamma$, then which of the following options is/are correct?
JEE AdvancedJEE Advanced 2019
Solution:
Let point $P(x, y)$
Equation of tangent at $P$;
$Y-y=\frac{dy}{dx}\left(X-x\right)$
So $Y_{P}\left(0,y-x \frac{dy}{dx}\right)$
$PY_{P}=\sqrt{x^{2}+\left(x \frac{dy}{dx}\right)^{2}}=1$
$\Rightarrow \frac{dy}{dx}=\pm \frac{\sqrt{1-x^{2}}}{x}$
$\Rightarrow dy=\pm\left(\frac{\sqrt{1-x^{2}}}{x}\right)dx \,let x = sin\theta, dx = cos\theta d\theta$
$\Rightarrow dy=\pm\left(cosec\theta-sin\theta\right)d\theta$
$\Rightarrow y=\pm\left[-In\left(cosec\theta-cot\theta\right)+cos\theta\right]+C$
$\Rightarrow y=\pm\left[-In\left(cosec\theta+cot\theta\right)+cos\theta\right]+C$
$y=\pm\left[-In\left(\frac{1+\sqrt{1-x^{2}}}{x}\right)+\sqrt{1-x^{2}}\right]+C$
As the curve lies in the $1^{st}$ quadrant so y must be positive
$y=In\left(\frac{1+\sqrt{1-x^{2}}}{x}\right)-\sqrt{1-x^{2}}+C$
$\because y\left(1\right)=0 \Rightarrow C=0$
$\Rightarrow y=In\left(\frac{1+\sqrt{1-x^{2}}}{x}\right)-\sqrt{1-x^{2}}$
Also the correct differential equation will be
$\frac{dy}{dx}=-\frac{\sqrt{1-x^{2}}}{x}$
$\Rightarrow xy '+\sqrt{1-x^{2}}=0$