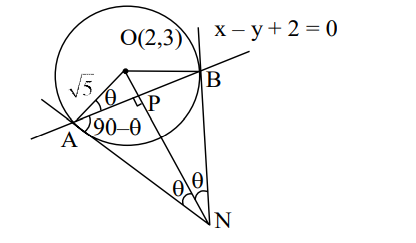Q. Let the tangent to the circle $C _{1}: x^{2}+y^{2}=2$ at the point $M(-1,1)$ intersect the circle $C_{2}$ : $( x -3)^{2}+(y-2)^{2}=5$, at two distinct points $A$ and $B$. If the tangents to $C _{2}$ at the points $A$ and $B$ intersect at $N$, then the area of the triangle $ANB$ is equal to :
Solution: