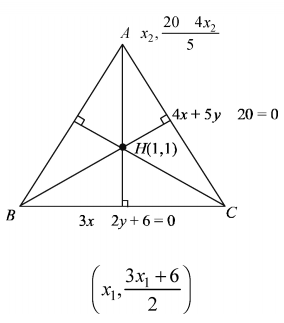
Question

Let the equations of two sides of a triangle be $3x - 2y + 6 = 0$ and $4x + 5y - 20 = 0$. If the orthocentre of this triangle is at $(1, 1)$ and the equation of its third side is $ax + by + c = 0$, then $a + b - c$ is

Answer 1

Since, $AH$ is perpendicular to $BC$
Hence, $m_{AH} . m_{BC} = -1$
$\left(\frac{\frac{20-4x_{2}}{5} -1}{x_{2}-1}\right)\times\frac{3}{2} = -1 $
$ \frac{15-4x_{2}}{5\left(x_{2} -1\right)} = -\frac{2}{3} $
$45 - 12 x_{2} = -10 x_{2 } + 10 $
$ 2x_{2} = 35 \Rightarrow x_{2} = \frac{35}{2} $
$\Rightarrow A\left(\frac{35}{2}, -10\right) $
Since, $BH$ is perpendicular to $CA$.
Hence, $m_{BH} \times m_{CA} = -1$
$\left(\frac{\frac{3x_{1}}{2} + 3-1}{x_{1} -1}\right)\left( - \frac{4}{5}\right) = -1 $
$\frac{\left(3x_{1} + 4\right)}{2\left(x_{1} - 1\right)}\times 4 = 5 $
$ \Rightarrow 6x_{1} + 8 = 5x_{1} - 5 $
$ \Rightarrow x_{1} = -13$
$ \Rightarrow \left(-13, \frac{-33}{2}\right)$
$\Rightarrow $ Equation of line $AB$ is
$y + 10 = \left(\frac{\frac{-33}{2} + 10}{-13-35}\right)\left( x - \frac{35}{2}\right)$
$\Rightarrow -16y - 610 = -13 x + \frac{455}{2} $
$\Rightarrow -122y - 1220 = -26 x + 455 $
$ \Rightarrow 26 x - 122 y - 1675 = 0$
Equation of third sideis $26x - 122y - 1675 = 0$
$\Rightarrow ax + by + c = 26x - 122y - 1675$
$a = 26, b = -122, c = - 1675$
$\therefore a + b - c = 26 + (-122)-(-1675)$
$= 1579$