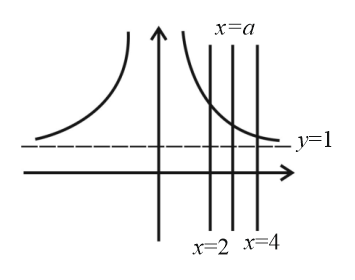
Question

Let the area bounded by the $x$ -axis, curve $y=\left(1 + \frac{8}{x^{2}}\right)$ and the ordinates $x=2$ and $x=4$ is ''$A$'' sq. unit and if the ordinate $x=a$ divides the area into two equal parts, then the correct statement among the following is

• A. $A=3$ and $a=2$
• B. $A=2$ and $a=1$
• C. $A=4\sqrt{2}$ and $a=\sqrt{2}$
• D. $A=4$ and $a=2\sqrt{2}$

Answer 1

Answer: (D)

$y=1+\frac{8}{x^{2}}$


Required area $A=\int\limits _{2}^{4}ydx=\int\limits _{2}^{4}\left(1 + \frac{8}{x^{2}}\right)dx$
$=\left[x - \frac{8}{x}\right]_{2}^{4}=4$
If $x = a$ bisects the area then we have $\int\limits _{2}^{a}\left(1 + \frac{8}{x^{2}}\right)=\frac{4}{2} \, \, \, \ldots \left(1\right)$
Now $\int\limits _{2}^{a}\left(1 + \frac{8}{x^{2}}\right)dx=\left[x - \frac{8}{x}\right]_{2}^{a}=\left[a - \frac{8}{a} - 2 + 4\right]$
Now $a-\frac{8}{a}+2=2 \, $ (by equation (1))
$\Rightarrow \, \, a-\frac{8}{a}=0 \, \, \Rightarrow \, \, a^{2}=8$
$\Rightarrow \, \, a = \pm 2 \sqrt{2}$
Since $2 < a < 4$
$\therefore \, \, a = 2 \sqrt{2}$