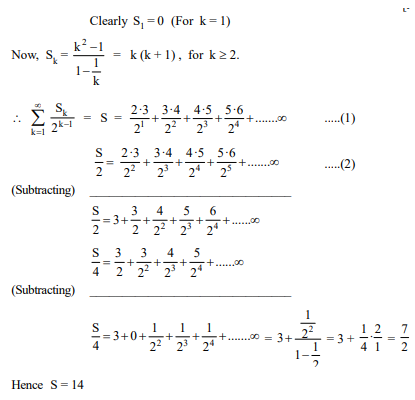
Q. Let $S _{ k }, k =1,2,3, \ldots \ldots$ denote the sum of infinite geometric series whose first term is $\left( k ^2-1\right)$ and the common ratio is $\frac{1}{k}$. Find the addition of the digits of sum $\displaystyle\sum_{k=1}^{\infty} \frac{S_k}{2^{k-1}}$.
Sequences and Series
Solution:
Correct answer is '5'