Q. Let S be the set of all straight lines in a plane. A relation R is defined on S by $aRb \Leftrightarrow a \bot b$ then R is :
Relations and Functions - Part 2
Solution:
We have to test the equivalencity of relation R on S.
(1) Reflexivity :
In a plane any line be parallel to itself not perpendicular. Hence aRb , R is not reflexive.
(2) Symmetry :
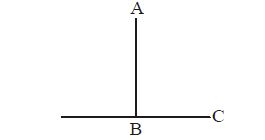
In a plane if a line AB is perpendicular to the other line BC, then BC is also perpendicular to AB, i.e.,
$aRb \Rightarrow AB \bot BC$
And $bRa \Rightarrow BC \bot AB$
Hence R is symmetric.
(3) Transitivity :
In a plane, let AB, BC and CA be three lines, such that
$AB \bot BC$ and $BC \bot CD$
$\Rightarrow AB || CD \Rightarrow a R b$, R is not transitive.
Hence, R is symmetric but neither reflexive nor transitive.