Question

Let $R=\left\{(x, y): x, y \in R , x^2+y^2 \leq 25\right\}$ $R^{\prime}=\left\{(x, y): x, y \in R , y \geq \frac{4}{9} x^2\right\} \text { then }$

• A. $\operatorname{dom} R \cap R^{\prime}=[-4,4]$
• B. range $R \cap R^{\prime}=[0,4]$
• C. range $R \cap R^{\prime}=[0,5]$
• D. $R \cap R^{\prime}$ defines a function.

Answer 1

Answer: (C)

The equation $x^2+y^2=25$ represents a circle with centre $(0,0)$ and radius 5 and the equation $y=\frac{4}{9} x^2$ represents a parabola with vertex $(0,0)$ and focus $(0,1 / 9)$.
Hence $R \cap R^{\prime}$ is the set of points indicated in the Fig.1.27
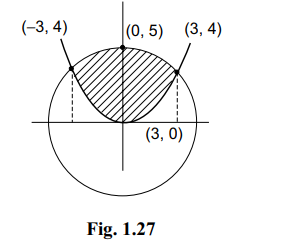$=\{(x, y):-3 \leq x \leq 3,0 \leq y \leq 3]\}$.
Thus dom $R \cap R^{\prime}=[-3,3]$ and range $R \cap R^{\prime}=[0,5] \supset[0,4]$
Since $(0,0) \in R \cap R^{\prime}$ and $(0,5) \in R \cap R^{\prime}$
$\therefore 0$ is related to 0 as well as 5 .
Hence $R \cap R^{\prime}$ doesn't define a function.